Fit and Diverse: Set Evolution
for Inspiring 3D Shape Galleries
Kai Xu1,2,
Hao Zhang3, Daniel Cohen-Or4,
Baoquan Chen1
1Shenzhen VisuCA Key
Lab/Shenzhen Institues of Advanced Technology, 2National
University of
Defense Technology,
3Simon
Fraser University, 4Tel
Aviv University
ACM Transactions
on Graphics (SIGGRAPH 2012), 31(4)
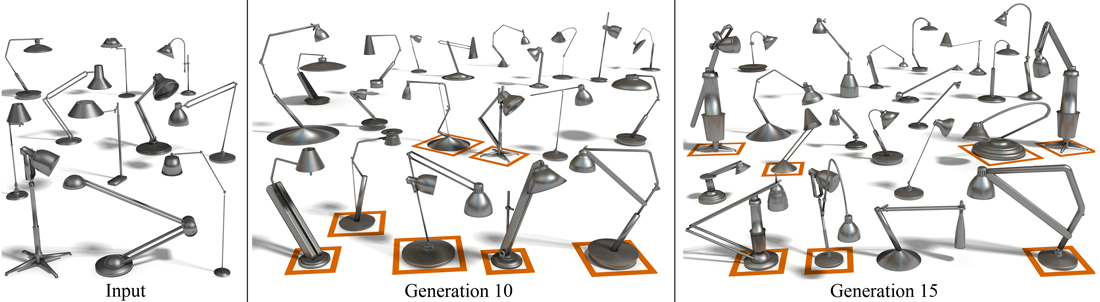
Figure 1: Set evolution
starting from a small input set of lamps (left). With the set evolution
"fit and diverse", new generations of shapes are
not only fit to be lamps but also exhibit significant and potentially
inspiring variations.
|
Abstract
|
We introduce set evolution as a
means for creative 3D shape modeling, where an initial population of 3D
models is evolved to produce generations of novel shapes. Part of the
evolving set is presented to a user as a shape gallery to offer
modeling suggestions. User preferences define the fitness for the
evolution so that over time, the shape population will mainly consist
of individuals with good fitness. However, to inspire the user's
creativity, we must also keep the evolving set diverse. Hence the
evolution is "fit and diverse", drawing motivation from evolution
theory. We introduce a novel part crossover operator which works at the
finer-level part structures of the shapes, leading to significant
variations and thus increased diversity in the evolved shape
structures. Diversity is also achieved by explicitly compromising the
fitness scores on a portion of the evolving population. We demonstrate
the effectiveness of set evolution on man-made shapes. We show that
selecting only models with high fitness leads to an elite population
with low diversity. By keeping the population fit and diverse, the
evolution can generate inspiring, and sometimes unexpected, shapes.
|
|
|
Paper |
|
|
|
Slides |
|
|
|
Video |
|
|
|
| Images |
Figure
2: The evolving population (left) consists of a diverse
background set (in gray) and a fit foreground set (in gold). The
gallery of shapes that is presented to the user is illustrated on the
right, which consists of shapes taken from the foreground set. [Back
Cover Image of SIGGRAPH 2012 Proceedings]
Figure
3: Color-coded visualization of fuzzy part correspondence (red
color: larger FPC value; yellow: small).
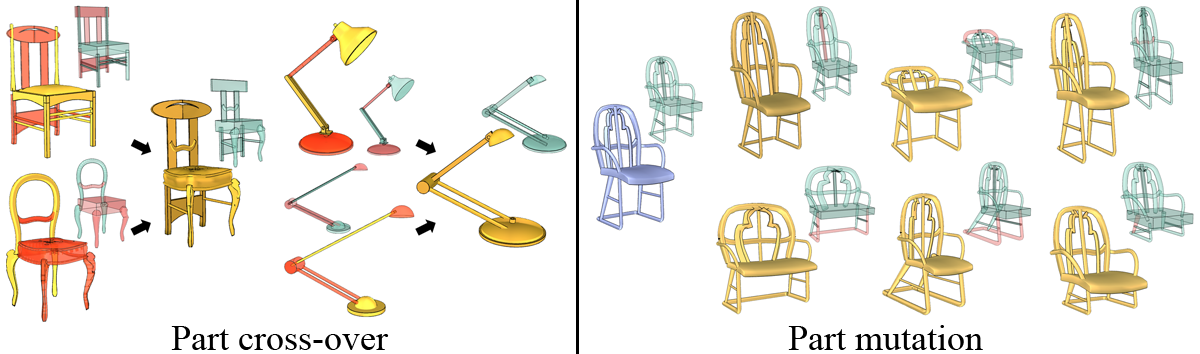
Figure
4: Part crossover (left) and part mutation (right) based on
component-wise controllers.
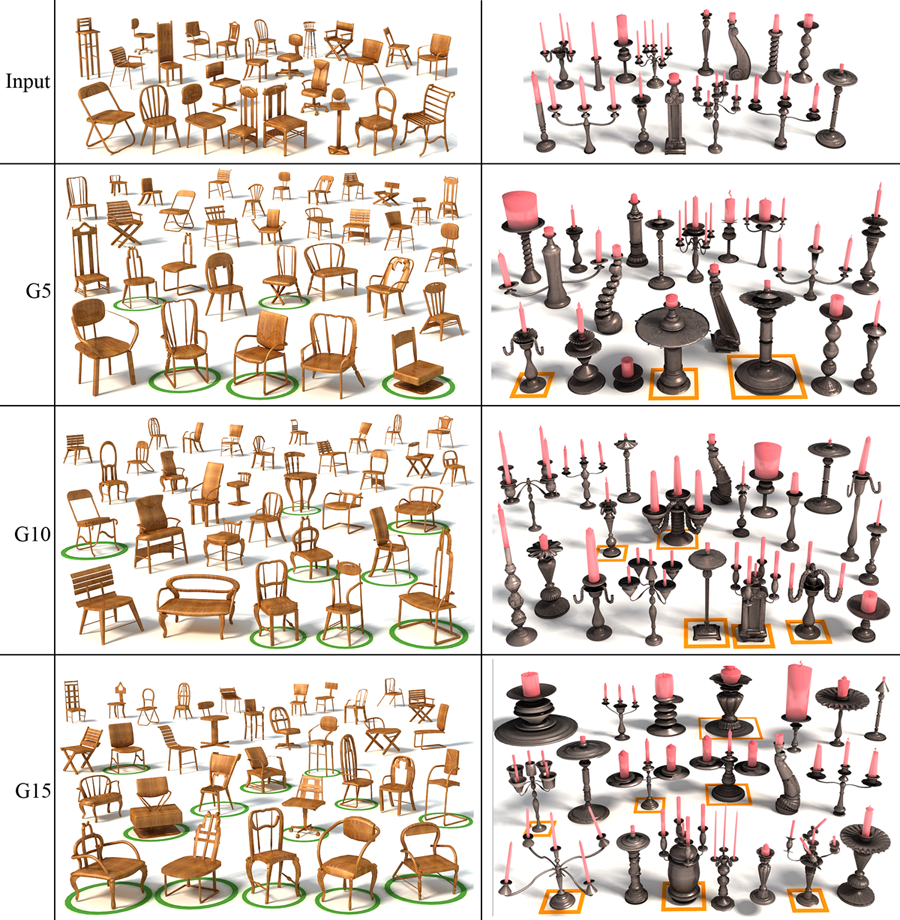
Figure
5:
Evolutions of a chair set (left) and a candelabrum set (right). The
entire input sets are shown. We show randomly selected shapes
from the gallery in three generations. Shapes marked are those
identified as unexpected/interesting by the participants.
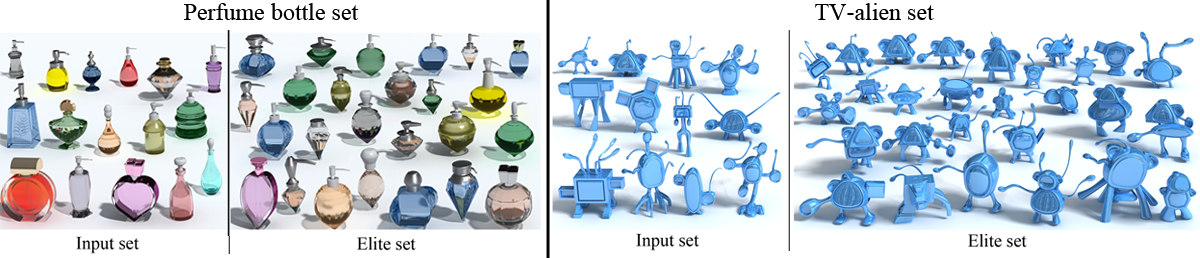
Figure
6: Elite sets generated due to a lack of diversity control.
(Left) Preferences given to heart- or diamond-shaped bottles. (Right)
Preferences given to cat-like creatures.
|
|
|
| Thanks |
We would first like to thank the
anonymous reviewers for their valuable feedback. Thanks also go to Chao
Lai and Shuai Lin from NUDT for their help with making the video and to
the artists from SIAT, especially Jiacheng Ren and Qifeng Wei, for the
modeling and rendering efforts. This work is supported in part by
grants from NSFC (61161160567, 61025012), National 863 Program
(2011AA010503), Shenzhen Science and Innovation Program
(CXB201104220029A, JC201005270329A), NSERC (No. 611370), and the Israel
Science Foundation.
|
|
|
| Data |
We provide the datasets (including both the input sets and the synthesized sets) appearing in the paper:
Full dataset (zip, 322M)
- Perfume bottles: input (40 OBJs, 21MB); synthesis (53 OBJs, 66MB)
- Candelabra: input (15 OBJs, 12MB); synthesis (61 OBJs, 74MB)
- Chairs: input (24 OBJs, 7MB); synthesis (96 OBJs, 30MB)
- Lamps: input (11 OBJs, 3MB); synthesis (62 OBJs, 23MB)
-Teapots & vases: input (27 OBJs, 27MB); synthesis (83 OBJs, 82MB)
-TV-aliens: input (12 OBJs, 3MB); synthesis (61 OBJs, 16MB)
|
|
|
| Bibtex |
@article
{xu_sig12,
title = {Fit and Diverse: Set Evolution for
Inspiring 3D Shape Galleries},
author
= {Kai Xu and Hao Zhang and Daniel Cohen-Or and Baoquan Chen}
journal
= {ACM Transactions on Graphics, (Proc. of SIGGRAPH 2012)},
volume
= {31},
number
= {4},
pages
= {57:1--57:10},
year
= {2012}
}
|
|